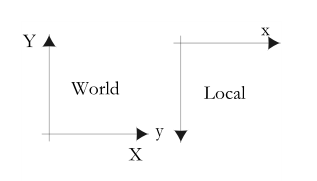
I found it useful to work out the 2-D equations to transform coordinates between the world and the local coordinate systems for encoding into software programming functions.
A simple non-matrix example is show below.
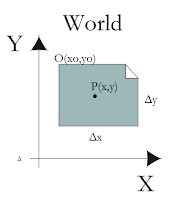
In the figure below, an image file has the origin O with the world coordinates (x0,y0) and dimensions of Δx and Δy.
The corresponding image file in the local coordinate system has the origin O'(x0',y0') and dimensions of Δx' and Δy'. Typically (x0',y0') = (0,0).
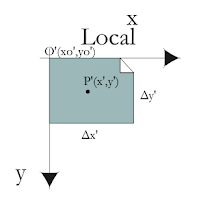
A point P(x,y) in the world coordinate system can be transformed to a point P'(x',y') in the local coordinate system with the following equations:
x' = (x - x0) * Sx
y' = -(y - y0) * Sy
where
Sx = Δx'/Δx
Sy = Δy'/Δy
A point P'(x',y') in the local coordinate system can be transformed to a point P(x,y) in the world coordinate system with the following equations:
x = (x'/Sx) + x0
y = -(y'/Sy) + y0

No comments:
Post a Comment