Octave (an open source software alternative to Matlab. See https://www.gnu.org/software/octave/) has the tools to determine the 3x3 transformation matrix. This post shows how to perform the calculation.
Given the 3 original measured 3D points X:
x1 = (2, -1, 2)
x2 = (-1, 2, 2)
x3 = (2, 2, -1)
And the 3 measured destination 3D points Y:
y1 = (-2, -9, -30)
y2 = (-23, 12, 9)
y3 = (13, 6, -6)
- First, write out the transformation and coordinates in the following form
AX=Y
where A is the unknown transformation matrix,
X is a matrix of the original coordinates formed by concatenating the points as column vectors X = [x1, x2, x3]
Y is a matrix of the destination coordinates formed by concatenating the points as column vectors Y = [y1, y2, y3] - Run Octave. In the command prompt, enter the X matrix values:
$> X = [2 -1 2; -1 2 2; 2 2 -1]
- In the prompt, enter the Y matrix values:
$> Y = [-2 -23 13; -9 12 6; -30 9 -6]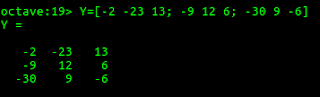
- Now calculate the inverse of X by typing the following into the prompt.
$> IX = inv(X)
- The transformation matrix A can be calculated by simply multiplying the matrix Y with the inverse of X. Type in the following at the prompt:
$> A = Y * IX
- Optional. Use the calculated matrix A and multiply with the original coordinates X and check whether the resultant values matches the measured Y coordinates.

No comments:
Post a Comment